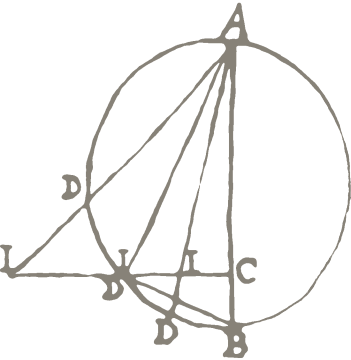
In seventeenth-century Europe, mathematicians were scholars. This project focuses on how early modern mathematicians read ancient Greek mathematics and used it to produce new mathematics. Research is organized around the early modern commonplace of “Greek analysis”—the idea that ancient mathematicians used a heuristic method, similar to symbolic algebra, in order to make their discoveries. Versions of this idea were central to the mathematical ambitions, and even practices, of mathematicians including François Viète, René Descartes, John Wallis, Isaac Newton, and Gottfried Leibniz. Studying these figures sheds light on the interplay of method and erudition as two distinct, both complementary and contradictory means of producing knowledge in the early modern period. The very different values these mathematicians placed on the emulation of classical mathematics, and the intellectual tools needed to realize it, expressed their disagreements about the nature of mathematical understanding and the kinds of intellectual communities conducive to it. By highlighting humanist aspects of the development of algebra and calculus, this project frames the scientific revolution as a continuation of the Renaissance. Continuities were not limited to shared texts and practices: seventeenth-century attitudes about the progress of knowledge were modifications of sixteenth-century attitudes about the recovery of classical culture. By constructing a history of mathematics, highly skilled mathematicians rendered their own techniques and those of others new or old, progressive or reactionary, universal or particular, good or bad.
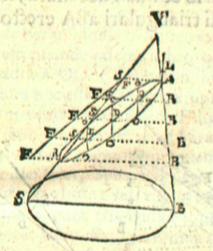
The ellipse considered as a section of the cone, from John Wallis's treatise On conic sections (1656). ETH-Bibliothek Zürich, Rar 246: 2. http://dx.doi.org/10.3931/e-rara-38681
Project
(2017-2018)